



Next: Smooth functions between manifolds
Up: The tangent space.
Previous: Submanifolds
Contents
If  is a submanifold then there is a natural
notion of the plane tangent to
is a submanifold then there is a natural
notion of the plane tangent to  at any point
at any point  independent of abstract notions such as equivalence
classes of paths and co-ordinates. It is just
the subspace of
independent of abstract notions such as equivalence
classes of paths and co-ordinates. It is just
the subspace of
 tangential to
tangential to  at
at  .
More precisely if
.
More precisely if
 it is the kernel
of
it is the kernel
of  which we denoted by
which we denoted by 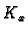 . To relate
this to the abstract notion of tangent
vector consider a smooth path
Because
. To relate
this to the abstract notion of tangent
vector consider a smooth path
Because
 this is naturally
a path in
this is naturally
a path in
 . We check first that this is smooth.
To do this choose co-ordinates
. We check first that this is smooth.
To do this choose co-ordinates  for
for
 about
about  satisfying
and denote by
satisfying
and denote by 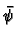 the corresponding co-ordinates
on
the corresponding co-ordinates
on  . Smoothness of
. Smoothness of  means that
the functions
means that
the functions
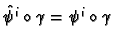 are smooth for each
are smooth for each
 . Because
. Because
 has image inside
has image inside  we also have that
we also have that
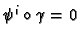 for each
for each
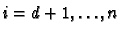 and hence these are also smooth. So
and hence these are also smooth. So  is a
smooth path in
is a
smooth path in
 .
Consider the vector
.
Consider the vector
 in
in
 . We have that
. We have that
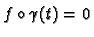 for all
for all 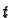 so by the chain rule
so by the chain rule
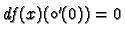 so that
so that
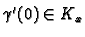 .
.
We can now define a map
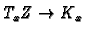 .
If
.
If
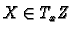 then we choose a path
then we choose a path  whose tangent vector at 0 is
whose tangent vector at 0 is  and map
and map  to
to
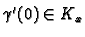 .
We have to check first that this is well-defined.
Let
.
We have to check first that this is well-defined.
Let  be another such path and consider the
co-ordinates
be another such path and consider the
co-ordinates 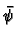 . By definition we have
. By definition we have
for every
 .
Hence we also have
for every
.
Hence we also have
for every
 . But
for
. But
for
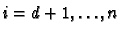 so we have
for
so we have
for
 . Hence
. Hence  maps to
the same element of
maps to
the same element of 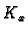 whether we use
whether we use
 or
or  . To show
that this map is injective we use a similar argument.
It is easy to see that this map is linear. Hence,
counting, dimensions we see that this is a linear
isomorphism.
. To show
that this map is injective we use a similar argument.
It is easy to see that this map is linear. Hence,
counting, dimensions we see that this is a linear
isomorphism.
We conclude that if
 is a submanifold and
we consider the tangents to all the paths through
is a submanifold and
we consider the tangents to all the paths through  ,
thought of as maps into
,
thought of as maps into
 then they span the space
then they span the space
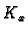 .
.




Next: Smooth functions between manifolds
Up: The tangent space.
Previous: Submanifolds
Contents
Michael Murray
1998-09-16
![]() .
If
.
If
![]() then we choose a path
then we choose a path ![]() whose tangent vector at 0 is
whose tangent vector at 0 is ![]() and map
and map ![]() to
to
![]() .
We have to check first that this is well-defined.
Let
.
We have to check first that this is well-defined.
Let ![]() be another such path and consider the
co-ordinates
be another such path and consider the
co-ordinates ![]() . By definition we have
. By definition we have
![]() is a submanifold and
we consider the tangents to all the paths through
is a submanifold and
we consider the tangents to all the paths through ![]() ,
thought of as maps into
,
thought of as maps into
![]() then they span the space
then they span the space
![]() .
.